Original :Ned Wright's
Cosmology Tutorial
Part 1: Observations of
Global Properties
Part 2: Homogeneity and Isotropy;
Many Distances; Scale Factor
Part 3: Spatial Curvature;
Flatness-Oldness; Horizon
Part 4: Inflation; Anisotropy and
Inhomogeneity
Bibliography
www.astro.ucla.edu/~wright/cosmolog.htm
Cours de
Cosmologie par le professeur Edward. L. Wright
Cours Cosmologie première partie
Cours Cosmologie deuxième partie
Cours Cosmologie troisième partie
Cours Cosmologie quatrième partie
Traduction libre : Jacques FRIC qui endosse toute la responsabilité de sa traduction vis à vis des erreurs qu'il aurait pu introduire. Commentaires
personnels [ …]
Cours de
Cosmologie : première partie
Il y a quelques centaines d'années l'univers se limitait au système solaire et la découverte que la Terre n'était pas au centre du système solaire (not the center) a été un pas important dans le développement de la Cosmologie. Au début du 20 ième siècle Shapley montra que le système solaire est loin du centre de la voie lactée (far from the center). Ainsi vers 1920 le décor était établi et prêt à recevoir les découvertes cruciales qui ont conduit au modèle du Big bang de l'Univers.
Observations critiques
En 1929 Hubble [1, 2, 3] déclara ( claim ) que les vitesses radiales des galaxies étaient proportionnelles à leur distance. Le décalage spectral ( vers le rouge) est une mesure de sa vitesse radiale de fuite et peut être mesuré à l'aide d'un spectromètre pour calculer le décalage Doppler. (Doppler shift). L'abaque ci dessous reprend les données de Hubble en 1929 :
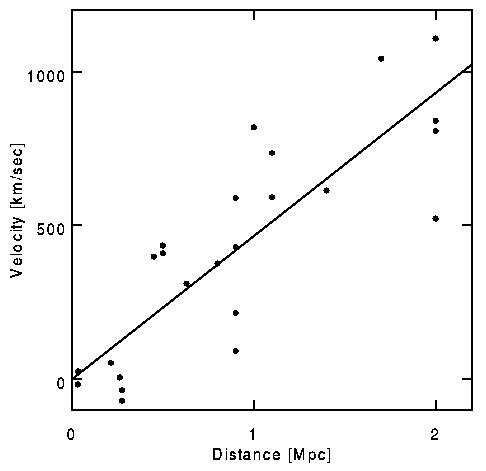
La pente de la ligne interpolée qui est de 464 km/sec/Mpc, est appelée
constante de Hubble constant, Ho. [Quelquefois j'utilise le
mode "TeX" , alors A_x
indique que x est un indice, Ax, alors que A^x indique que x est un
exposant, Ax.] comme les kilomètres et les Mégaparsecs (1 Mpc =
3.086E24 cm [le "E24" signifie 3.086 multiplié par 10 à la puissance
24]) sont des unités de distance, les unités simplifiées de Ho sont 1/temps, et la conversion
est donnée par :
1/Ho = (978 Giga-années)/(Ho en km/sec/Mpc)
Donc l'inverse de la valeur de la constante de Hubble est environ de 2 Ga ( 2 Gyr) . Ceci est censé être l'âge de l'Univers (age of the Universe), et nous savons ( et cela était connu en 1929) que l'âge de la terre est supérieur à 2 milliards d'années. Cette valeur de Ho, pour ce modèle cosmologique, fut accueillie avec le plus grand scepticisme et motiva le développement du modèle d'état stationnaire (Steady State). Cependant des travaux ultérieurs montrèrent que Hubble avait confondu deux types de Céphéides ( étoiles variables) utilisées pour étalonner les distances (distances,) et aussi que ce que Hubble croyait avoir identifié à des étoiles brillantes dans des galaxies lointaines étaient en fait des régions H II. Ces corrections conduisirent à diminuer la valeur de la constante de Hubble : Il y a actuellement principalement deux groupes qui utilisent les Céphéides: L'équipe ( HST Distance Scale Key Project) (Freedman, Kennicutt, Mould etal) qui a obtenu 68 à 78 km/sec/Mpc, tandis que le groupe Sandage, utilisant aussi les observations du HST des Céphéides pour étalonner les supernovae de Type Ia, a obtenu 57+/-4 km/sec/Mpc. D'autres méthodes pour déterminer l'échelle des distances s'appuient sur le retard temporal des lentilles gravitationnelles et l'effet Sunyaev-Zeldovich dans les amas distants : ces méthodes sont indépendantes de l'étalonnage par les Céphéides et donnent des valeurs cohérentes avec les moyennes de celles obtenues par les deux autres groupes utilisant le HST.: 65+/-8 km/sec/Mpc. De ces valeurs de Ho on déduit un âge 1/Ho de 15Ga. [ cf données récentes de WMAP]
Les données de Hubble en 1929 étaient en fait imprécises, du fait que les galaxies ont aussi des vitesses propres "erratiques" de plusieurs centaines de km/s alors que ses données n'allaient pas au delà de 1200 km/sec. Ceci a conduit certains a proposer une loi de type quadratique de décalage vers le rouge ( quadratic redshift-distance laws,) mais les données représentées ci dessous sur les supernovae de Type Ia par Riess, Press and Kirshner (1996)
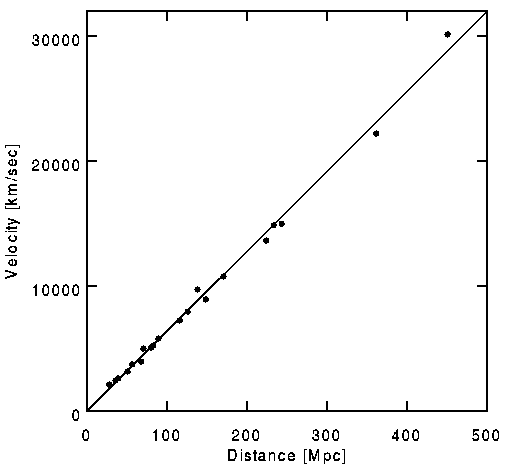
portant au delà de 30,000 km/sec nous
offrent une confirmation spectaculaire de la loi de Hubble.
v = dD/dt = H*D
La ligne interpolée dans ce graphique correspond à 64 km/sec/Mpc. Comme nous mesurons la vitesse radiale en utilisant l'effet Doppler cela est souvent appelé le décalage spectral ( vers le rouge) redshift. Ce décalage spectral "z" est défini tel que :
1 + z = lambda(observé)/lambda(émis)
où lambda est la longueur d'onde caractéristique d'une raie ou d'un motif dans le spectre d'un objet. La relativité nous dit (relativity ) que "z" est donné par:
1 + z = Ö((1+v/c)/(1-v/c)) so v = cz + ...
L'indice "o" dans Ho indique la valeur actuelle de cette variable dépendant du temps. Comme 1/Ho est approximativement l'âge de l'Univers , la valeur de H dépend du temps. Une autre variable d'indice 0 est to, l'âge de l'Univers.
La relation linéaire entre "z" et la distance est compatible avec le principe Copernicien : nous ne sommes pas dans une position privilégiée dans l'Univers. D'abord remarquons que la vitesse de récession est symétrique: Si A voit B s'éloigner, alors B voit A s'éloigner, comme montré dans ce diagramme ci dessous,
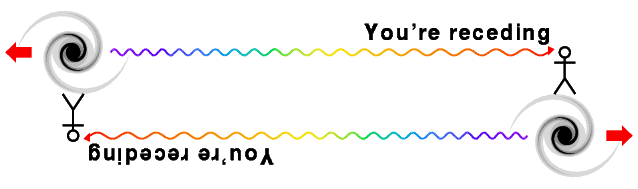
basé sur un croquis de Bob Kirshner. Considérons maintenant le diagramme
d'espace temps (space-time
diagram) montrant plusieurs galaxies voisines s'éloignant de nous de notre
point de vue. (galaxie A, la ligne d'univers bleue) en haut et du point de vue de
la Galaxie B (la ligne d'Univers verte) en bas.
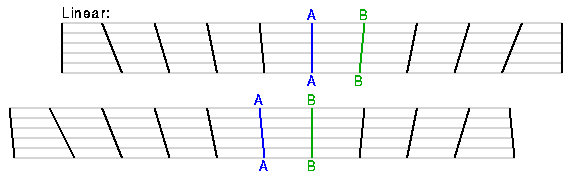
Ces diagrammes montrant différents points de vue sont identiques à l'exception
du nom des Galaxies. Une loi quadratique
v(sq) = D2 par contre se transforme en une loi non
quadratique anisotropique quand on change de point de vue comme montré ci
dessous.
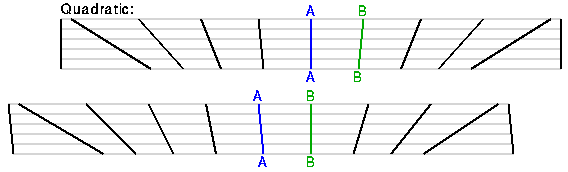
Donc si nous supposons une loi quadratique vitesse/distance [ par rapport à nous ], un observateur dans une autre
Galaxie va constater une loi différente qui va être différente dans les
différentes directions [ non isotrope]. Donc si
nous voyons une loi quadratique v(sq),
alors B verra des vitesses radiales plus élevées dans une direction que dans
l'autre [ + élevé
vers la droite sur la figure ci dessus]. Ceci conduit à un point
privilégié dans l'Univers, un "centre" , seul point d'où on voit une
loi de récession isotrope. directions. Comme nous constatons une loi de Hubble
isotrope soit nous sommes au centre de l'Univers, ce qui est anti- Copernicien
soit la loi est linéaire, seule possibilité pour être compatible avec
l'homogénéité et l'isotropie de l'Univers.
La loi de Hubble génère une expansion homogène (homologous expansion ) qui ne change pas la forme des objets alors que les autres lois possibles liant vitesse et distance conduisent à des distorsions pendant l'expansion. La loi de Hubble définit un référentiel privilégié en tout point de l'Univers. Un observateur en mouvement propre par rapport au "flot de Hubble" va observer des décalages vers le bleu dans la direction du mouvement et vers le rouge dans l'autre au lieu d'un décalage isotrope vers le rouge des galaxies. Nous pouvons donc observer notre mouvement par rapport au flot de Hubble, qui caractérise notre mouvement relatif par rapport à l'Univers observable. Un observateur co-mobile est au repos par rapport à ce référentiel privilégié. Notre système solaire n'est pas co-mobile, nous avons une vitesse relative de 370 km/sec. Le groupe local de galaxies, dans lequel la voie lactée est incluse laisse apparaître un mouvement relatif de 600 km/sec par rapport à l'Univers observable.
Hubble
mesura aussi le nombre de galaxies et leurs luminosités dans les différentes
directions du ciel. Il trouva environ le même nombre de galaxies peu brillantes
dans toutes les directions , même s'il y a excès important de galaxies
brillantes dans la partie nord du ciel. Quand une distribution est la même dans
toutes les directions, elle est isotrope. Ensuite il observa les
galaxies de luminosité apparente supérieure à F/4 , et il en compta 8 fois
plus que de galaxies de luminosité
apparente supérieure à F. Comme une luminosité divisée par 4 correspond à une
distance double [ loi en inverse carré de la
distance], le volume correspondant est 8 fois plus grand, son observation
confirme donc l'homogénéité approchée ( densité uniforme) de
l'Univers à grande échelle .
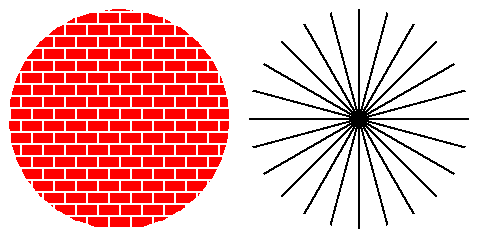
La figure ci dessus montre un motif homogène mais non isotrope à gauche et
isotrope mais non homogène à droite. Si une figure est isotrope en plus d'un point
(deux sur une sphère) , elle est de plus homogène.
Bien sûr l'Univers n'est qu'approximativement homogène et isotrope même à grande échelle, car il y a des régions notoirement plus denses comme la Terre. Mais il peut être statistiquement homogène et isotrope comme le montre un champ simulé de galaxies après lissage des détails (24 kB simulated galaxy field ).
Peacock and Dodds (1994, MNRAS, 267, 1020) ont examiné les proportions de fluctuation de densité dans l'Univers proche, fonction du rayon de la région considérée et après passage par un filtre " haut de forme", ils ont trouvé:
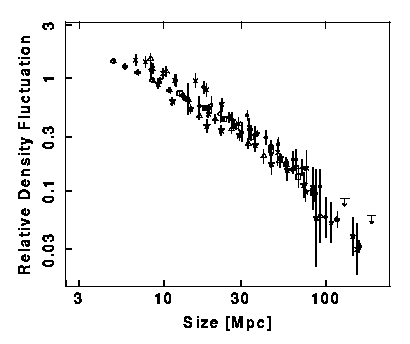
Pour des régions de 100 Mpc, l'Univers est homogène à quelques % près. Des
études sur le décalage spectral .( Redshift surveys) de
régions très grandes ont confirmé cette tendance vers une homogénéité
croissante lorsque l'échelle s'accroît.
L'hypothèse d'isotropie et d'homogénéité de l'Univers s'est trouvée confortée après que Penzias et Wilson eurent découvert le rayonnement de fond cosmologique (RFC) en1965. Il ont observé un rayonnement isotrope, provenant de toutes les directions du ciel, de 7.5 cm de longueur d'onde de type "corps noir" équivalent à une température de 3.7+/-1 degrés Kelvin à l'époque.[ 2,725 K selon WMAP] [Les degrés Kelvin ont la même échelle que les degrés Celsius mais leur référence est le zéro absolu, ainsi la glace fond à 273.15 K.] Un corps noir absorbe tous les rayonnements qu'il reçoit et a une température constante. Les caractéristiques du RFC ont été mesurées par de nombreuses expériences. Ci dessous les mesures faites l'instrument FIRAS sur le satellite COBE [ confirmé et amélioré par WMAP]:
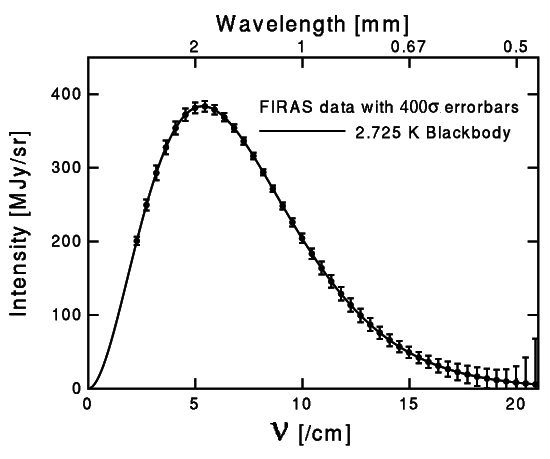
Sur l'axe des x, on représente
l'inverse de la longueur d'onde en 1/[longueur d'onde en cm]. Sur l'axe des y ,
on représente la puissance par unité de surface par unité de fréquence [ dans des bandes de largeur constante], par unité
d'angle solide en Méga-Janskies par stéradian. 1 Jansky
vaut 10-26 Watts par mètre
carré par Hertz. Les barres d'erreurs ont été dilatées d'un facteur 400, on
peut ainsi voir l'excellente adéquation avec le spectre de rayonnement d'un
corps noir à une température To = 2.725 K.
La température du RFC est Presque la même dans tout le ciel. . La figure ci dessous montre cela avec une échelle linéaire de gris telle que 3°K est blanc et 0°K est noir..
On voit que le rayonnement est presque parfaitement isotrope. Ces observations
confortent le principe Cosmologique.
L'Univers est Homogène et Isotrope
Un autre élément favorable au big bang est l'abondance des éléments légers tels que l'hydrogène, le deutérium ( hydrogène lourd) l'hélium et le lithium. Pendant l'expansion les photons du RFC perdent de l'énergie du fait du décalage vers le rouge et le RFC se refroidit. Vu à l'envers, ceci signifie que la température du RFC était très élevée dans le passé. Quand il était âgé de seulement quelques minutes, la température était suffisamment élevée pour produire ces éléments légers par fusion nucléaire.. La théorie de la Nucléosynthèse du Big bang (Big Bang Nucleosynthesis) prédit qu'environ1/4 de la masse de l'Univers doit être constituée d'hélium, ce qu'on observe approximativement. L'abondance du deutérium est inversement proportionnelle à la densité de nucléons (nucleons) dans l'univers, et l'abondance observée de deutérium correspond à un nucléon pour 4 à 7 mètres cubes d'espace de l'Univers.
FAQ | Tutorial : Part 1 | Part 2 | Part 3 | Part 4 | Age | Distances | Bibliography | Relativity
© 1996-2001 Edward L. Wright. Last modified 9-Mar-2001