Original : Ned Wright Cosmology tutorial, part 2

Cours de Cosmologie par le professeur Edward L. Wright

www.astro.ucla.edu/~wright/cosmolog.htm

Cours Cosmologie première partie

Cours Cosmologie deuxième partie

Cours Cosmologie troisième partie

Cours Cosmologie quatrième partie

Cours de Cosmologie : Deuxième partie

Traduction libre par J. Fric qui endosse la responsabilité des erreurs que sa traduction aurait pu introduire. Commentaires personnels entre […]

Retour vers première partie

Homogènéité et Isotropie

Le principe cosmologique:

L'Univers est homogène et isotrope

Dire que l'Univers est homogène signifie que toutes les caractéristiques mesurables de l'univers sont les mêmes partout. Ceci n'est qu'approximativement vrai, mais cela se révèle être une excellente approximation sur des domaines très étendus. Comme l'âge de l'Univers est une caractéristique observable, l'homogénéité de l'univers doit se retrouver sur une surface de temps propre constant depuis le Big bang. La dilatation temporelle fait que le temps propre mesuré par un observateur dépend de la vitesse de cet observateur, donc nous précisons que la variable de temps t de la loi de Hubble est le temps propre écoulé depuis le Big Bang pour des observateurs comobiles.

Vous avez dit distance ? : Quelles distances ?

La loi de Hubble (v = HD) est vraie pour toutes les valeurs de D, même très grandes qui donnent v > c, sous réserve d'interpréter correctement la distance D et la vitesse v. La distance de la loi de Hubble est définie telle que si A et B sont deux galaxies distantes que nous voyons dans la même direction et qu'elles ne sont pas trop éloignées l'une de l'autre alors la différence des distances qui nous séparent D(B)-D(A), est la distance de A à B que A mesurerait. Mais cette mesure doit être faite " maintenant", donc A doit faire cette mesure au même temps propre depuis que le big bang que celui que nous constatons en ce moment. Donc pour déterminer la distance D d'une galaxie Z, nous devons trouver une " chaîne " de galaxies ABC...XYZ le long du chemin vers Z dont chacun des éléments est proche de ses voisins et faire que chaque galaxie mesure la distance vers sa galaxie qui lui succède au même temps t_o depuis le Big Bang. La distance de Z, D(de nous à Z), est la somme de tous ces petits intervalles.:

D(de nous à Z) = D(de nous à A) + D(A à B) + ... D(X à Y) + D(Y à Z)

La vitesse dans la loi de Hubble est alors la variation de D par unité de temps. C'est environ cz pour les petits décalages vers le rouge (redshifts) mais s'en écarte pour les grands. Le diagramme d'espace temps ( space-time diagram ) ci dessous reproduit l'exemple du premier chapitre 1 (Part 1) montrant comment le changement de point vue, lié au passage d'un observateur A à un observateur B, conserve la vitesse linéaire par rapport à la distance de la loi de Hubble.

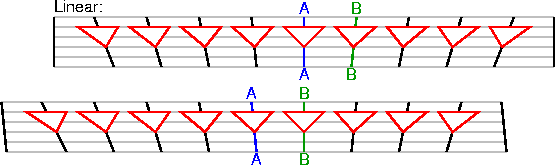
linear v-vs-D
space-time with lightcones

mais nous avons ajouté cette fois les cônes de lumière. Remarquons que les cônes de lumière doivent s'incliner avec les lignes d'univers, montrant qu'avec ces variables cosmologiques la vitesse de la lumière est "c" par rapport aux observateurs locaux co-mobiles.

La loi de Hubble utilise des coordonnées de temps "t" et de distance "x" qui ne sont pas les mêmes qu'en Relativité Restreinte, ce qui est souvent source de confusion. En particulier des Galaxies suffisamment éloignées de nous ont des vitesses d'éloignement supérieures à celle de la lumière.

Les cônes de lumière des galaxies distantes représentées dans le diagramme ci dessus sont inclinés au delà de la verticale indiquant v > c. Le diagramme d'espace temps ci dessous ( space-time diagram) représente un modèle Cosmologique de densité " zéro" ( en fait de densité très faible) qui utilise les coordonnées "D" et "t" de la loi de Hubble.

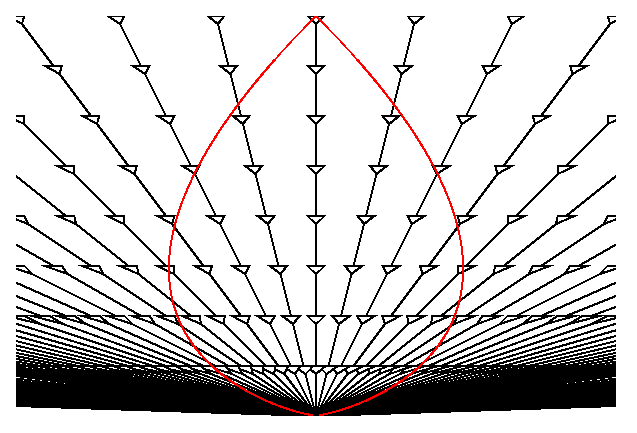
Omega=0 space-time

Les lignes d'Univers des observateurs co-mobiles sont assorties et "décorées" de petits cônes de lumières schématiques. La courbe rouge en forme de poire est notre "cône " du passé [ qui tient compte de l'expansion, d'où la forme]. Remarquons que cette courbe rouge a localement la même pente que les petits cônes de lumière [ RR oblige ]. Dans cette représentation les vitesses supérieures à "c" sont possibles et comme les Univers ouverts sont spatialement infinis, elles sont en fait nécessaires. Il n'y a pas de contradiction avec la Relativité Restreinte qui stipule que rien ne peut aller plus vite que la lumière, du fait que dans ce diagramme les " vitesses" sont définies à partir d'autres coordonnées "t" et "x" que celles de la RR. Si on représente le même diagramme d'espace temps dans les coordonnées "x" et "t" de la Relativité restreinte nous obtenons :

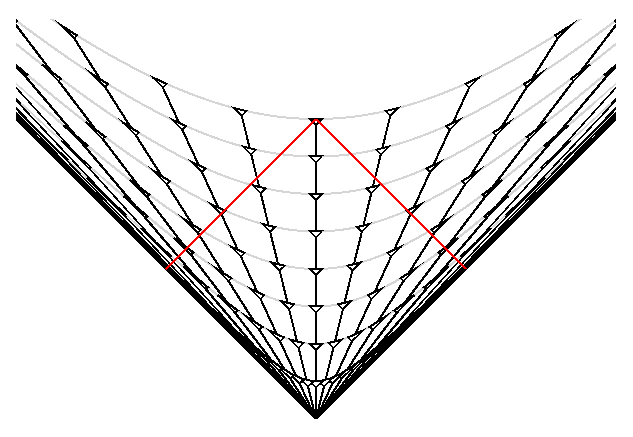
Omega=0 model in SR coordinates

Les hyperboles grises matérialisent les surfaces à temps propre constant depuis le Big Bang. Si nous les " redressons" pour obtenir le diagramme d'espace temps précédent, les lignes d'Univers des galaxies s'écartent et donnent des vitesses v = dD/dt éventuellement supérieures à "c".

Mais en coordonnées de la Relativité Restreinte les vitesses sont toujours inférieures à "c".

Nous voyons également sur ce diagramme que notre cône du passé [ un vrai cône cette fois ] coupe les lignes d'Univers des Galaxies les plus lointaines à la distance x = c*t_o/2, en coordonnées de Relativité Restreinte. Mais la distance de la loi de Hubble qui est mesurée maintenant [ sur l'hyperbole grise "du haut" qui correspond au "présent" ], de ces Galaxies les plus éloignées est infinie ( dans ce modèle). De plus ces Galaxies, à une "distance de Hubble" infinie et donc une vitesse liée à la loi de Hubble infinie, sont visibles pour nous, car dans cette représentation, l'univers observable est l'Univers entier. Les relations entre la distance de la loi de Hubble, sa vitesse (D & v) et le décalage vers le rouge " z" sont données ci dessous [ cas d'un Univers à densité asymptotiquement nulle]:

v = H_oD

D = (c/H_o)ln(1+z)

1+z = exp(v/c)

Remarquons que la loi décalage spectral / vitesse n'est pas celle de l'effet Doppler de la Relativité Restreinte.

1+z = [((1+v/c)/(1-v/c))]^1/2

Qui s'applique seulement en coordonnées de la Relativité Restreinte, pas en coordonnées " Cosmologiques".

Même si en principe la "distance de la loi de Hubble" est mesurable, la nécessité de disposer d'observateurs auxiliaires tout le long de la "chaîne " de galaxies menant à une Galaxie lointaine, la rend quasi impraticable. D'autres distances peuvent être mesurées plus facilement.

L'une d'entre elles, est la "distance de taille angulaire" définie par :

theta = taille/D_A    d'où   D_A = taille/theta

où la taille est la taille transversale,[supposée connue de façon absolue ], d'un objet et "theta" est l'angle (en radians) qu'il sous tend dans le ciel. Pour le modèle à densité zéro, la coordonnée "x" de la Relativité Restreinte est égale à la distance de taille angulaire, x = D_A.

Un autre indicateur important de distance est le flux lumineux reçu d'un objet, [dont la luminosité absolue est supposée connue ( chandelle standard)], ceci permettant de définir la distance de luminosité D_L par:

Flux = Luminosité/(4*pi*D_L²)

Une quatrième distance est définie à partir de son temps de parcours par la lumière: c*(t_o-t_em). Ceux qui disent que la plus grande distance à laquelle nous pouvons voir est c*t_o utilisent cette notion de distance. Mais c*(t_o-t_em) n'est pas une distance très utilisable, car il est difficile de déterminer t_em, l'âge de l'Univers auquel la lumière que nous recevons a été émise.

Finalement, le décalage spectral est un indicateur très important de distance, car les astronomes savent le mesurer facilement, alors que la taille ou la luminosité nécessaires pour calculer D_A ou D_L sont toujours très difficiles à déterminer. Le décalage spectral est l'indicateur de distance le plus précieux, injustement ignoré par les journalistes scientifiques ( il est vrai qu'il est représenté par la lettre "z" et que dans les écoles de journalismes, on ne va pas forcément aussi loin!).

La courbe représentant les relations entre ces différentes distances dépend du modèle cosmologique. L'abaque "décalage spectral" ( redshift) fonction de la distance pour les supernovae de Type Ia, donnée précédemment est en fait une abaque de "cz" fonction de "D_L", du fait que le flux lumineux est utilisé pour déterminer la distance des supernovae. Ces données éliminent les modèles qui ne donnent pas de relation linéaire entre" cz" et D_L pour "cz" petit . Ces observations ont été étendues à des supernovae plus éloignées (distant supernovae) pour mesurer la non linéarité de la relation en entre "cz" et D_L ( curvature of the cz vs D_L relation ) lorsque "cz" n'est plus petit, et ont apporté une information plus significative sur la nature de l'Univers.

Le RFC ( rayonnement de fond Cosmologique) ayant la caractéristique d'un corps noir parfait (blackbody) nous permet de déterminer la relation entre D_A et D_L. Comme le RFC que nous observons aujourd'hui, vient de loin, mais a toujours une nature de corps noir, un corps noir lointain doit ressembler à un corps noir (même si sa température peut être modifiée par le décalage spectral). La luminosité d'un corps est:

L = 4*pi*R²*sigma*T_em⁴

où R est le rayon, T_em est la température d'émission du corps noir et sigma est la constante de Stephan-Boltzmann. Observé à un décalage spectral "z" la température est :

T_obs = T_em/(1+z)

Et le flux est :

F = theta²*sigma*T_obs⁴

Où le rayon angulaire est lié au rayon physique par:

theta = R/D_A

En combinant ces équations on obtient:

D_L² = L/(4*pi*F)

    = (4*pi*R²*sigma*T_em⁴)/(4*pi*theta²*sigma*T_obs⁴)

    = D_A²*(1+z)⁴

ou

 D_L = D_A*(1+z)²

Les modèles qui ne présdisent pas cette relation entre D_A et D_L, tels que le modèle chronométrique (chronometric model) ou le modèle de la lumière fatiguée (tired light model) sont invalidées par les propriétés du RFC.

Ci joint un calculateur Javascript (Javascript calculator) qui à partir de H_o, Omega_M, la constante cosmologique normalisée (cosmological constant lambda) et le décalage spectral z calcule toutes ces distances.

Facteur d'échelle a(t)

Comme la vitesse ( dD/dt) est strictement proportionnelle à D, la distance entre deux objets co-mobiles s'accroît d'un facteur (1+H*dt) pendant l'intervalle de temps dt. Ceci signifie que nous pouvons écrire la distance entre deux observateurs co-mobiles comme suit:

D_G(t) = a(t)*D_G(t_o)

où D_G(t_o) est la distance actuelle à la galaxie G tandis que a(t) est un facteur d'échelle universel qui s'applique à tous les objets co-mobiles. De cette définition nous voyons que a(t_o) = 1.

Nous pouvons calculer la dynamique de l'Univers en considérant un objet à une distance D(t) = a(t) D_o. Cette distance et la vitesse correspondante dD/dt sont mesurées par rapport à nous, en nous considérant au centre du système de coordonnées. L'accélération gravitationnelle due à la boule de matière de rayon D(t) est g = -G*M/D(t)² où la masse est M = 4*pi*D(t)³*rho(t)/3. Rho(t) est la densité de matière qui ne depend que du temps du fait de l'homogénéité de l'Univers. La masse contenue jusqu'à une distance D(t) est indépendante du temps car la matière à l'intérieur à une vitesse expansion inférieure et reste donc à l'intérieur et celle à l'extérieur une vitesse supérieure et reste donc à l'extérieur. L'effet gravitationnel de la matière extérieure est nul: la gravitation à l'intérieur d'une coquille sphérique de matière est nulle, et toute la matière à l'extérieur [ plus loin que D(t) ] peut être représentée par un emboîtement de coquilles sphériques. Avec une masse intérieure à D(t) constante générant une accélération du bord , le problème se ramène à celui d'un corps à déplacement radial dans le champ de gravitation d'une masse ponctuelle. Si la vitesse est inférieure à la vitesse de libération, l'expansion va s'arrêter et l'univers se re-contracter. Si la vitesse est égale à la vitesse de libération (escape velocity ) c'est le cas critique. Ceci donne

v = H*D = v(esc) = Ö(2*G*M/D)

    H²*D² = 2*(4*pi/3)*rho*D²  ou

rho(crit) = 3*H²/(8*pi*G)

Pour rho inférieur ou égal à la densité critique (critical density) rho(crit), l'Univers s'étend à jamais, tandis que pour rho supérieur à rho(crit),l'Univers arrête son expansion et se re-contracte. La valeur de rho(crit) pour H_o = 65 km/sec/Mpc est de 8E-30 = 8*10^-30 gm/cc soit 5 protons par mètre cube soit 1,2.E11 = 1.2*10¹¹ masses solaires par Mégaparsec cube. Cette dernière valeur doit être comparée à la luminosité observée de 1.75E8 = 1.75*10⁸ luminosités solaires par Mpc³, ce qui exige un rapport masse/luminosité de 700 en unités solaires pour fermer l'Univers. Si la densité est proche de la densité critique, celà signifie que la majorité de la matière est trop sombre pour être observée. Les dernières estimations ( density estimates) suggèrent que la densité est proche de 1 [ WMAP], ce qui veut dire que la majorité de l'univers n'est pas visible [ Matière et énergie "sombre" : voir résultats récents de WMAP: 70% énergie sombre,26 % matière sombre, 4% matière visible]

Vers troisième partie

Ned Wright's home page